07. 练习:状态值函数
练习:状态值函数
在这道练习中,你将计算特定策略对应的值函数。
MDP 中的每个状态(共九个)都用 \mathcal{S}^+ = {s_1, s_2, \ldots, s_9 } 之一标记,其中 s_9 是终止状态。
思考下下图表示的(确定性)策略(角色部分)。
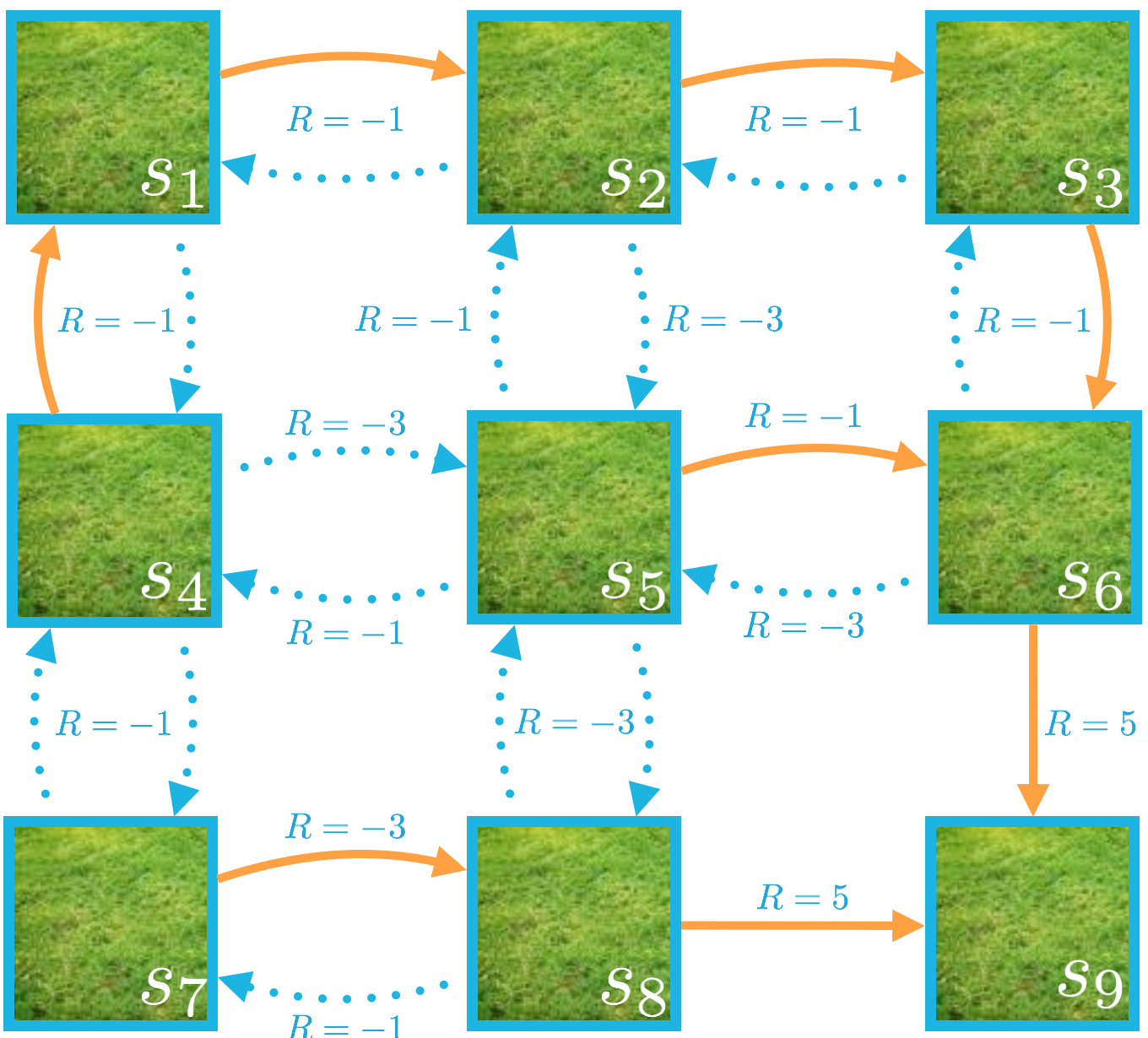
策略 \pi 由以下方程确定:
\pi(s_1) = \text{right}
\pi(s_2) = \text{right}
\pi(s_3) = \text{down}
\pi(s_4) = \text{up}
\pi(s_5) = \text{right}
\pi(s_6) = \text{down}
\pi(s_7) = \text{right}
\pi(s_8) = \text{right}
注意,因为 s_9 是一个终止状态,如果智能体从该状态开始,则该阶段立即结束。因此,智能体不需要选择动作(因此我们不会在策略中包含 s_9),并且 v_\pi(s_9) = 0。
现在花时间计算该策略对应的状态值函数 v_\pi。(你会发现贝尔曼预期方程可以为你节省大量工作!)
假设 \gamma = 1。
完成后,使用 v_\pi 回答以下问题。
问题 1
v_\pi(s_4) 是多少?
SOLUTION:
1问题 2
v_\pi(s_1) 是多少?
SOLUTION:
2问题 3
对于以下语句:
- (1) v_\pi(s_6) = -1 + v_\pi(s_5)
- (2) v_\pi(s_7) = -3 + v_\pi(s_8)
- (3) v_\pi(s_1) = -1 + v_\pi(s_2)
- (4) v_\pi(s_4) = -3 + v_\pi(s_7)
- (5) v_\pi(s_8) = -3 + v_\pi(s_5)
SOLUTION:
- (2)
- (3)